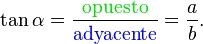El arte de las matemáticas: 2011

domingo, 20 de marzo de 2011

webquest "Thales y la proporcionalidad"

Para desarrollar la webquest propuesta debes hacer clik en el enlace
Thales y la propocionalidad

martes, 8 de marzo de 2011

Trigonometria básica ( 4to año)

Hola, bienvenidos a esta primera clase de su nuevo curso. Este es el primer tema del año. Este material les servirá de guia para resolver el trabajo práctico Nro1 cuyas consignas fueron recibidas en clase. Suerte¡¡.Cualquier duda la conversamos luego.

CONCEPTO DE TRIGONOMETRIA

La trigonometría es una rama de la matemática, cuyo significado etimológico es "la medición de los triángulos". Se deriva del vocablo griego τριγωνο <trigōno> "triángulo" + μετρον <metron> "medida".
En términos generales, la trigonometría es el estudio de las funciones seno, coseno; tangente, cotangente; secante y cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión. La trigonometría se aplica a otras ramas de la geometría, como es el caso del estudio de las esferas en la geometría del espacio.
Posee numerosas aplicaciones: las técnicas de triangulación, por ejemplo, son usadas en astronomía para medir distancias a estrellas próximas, en la medición de distancias entre puntos geográficos, y en sistemas de navegación por satélites.

Definiciones respecto de un triángulo rectángulo

Para definir las razones trigonométricas del ángulo:

α

, del vértice A, se parte de un triángulo rectángulo arbitrario que contiene a este ángulo. El nombre de los lados de este triángulo rectángulo que se usará en los sucesivo será:

La hipotenusa (h) es el lado opuesto al ángulo recto, o lado de mayor longitud del triángulo rectángulo.
El cateto opuesto (a) es el lado opuesto al ángulo que queremos determinar.
El cateto adyacente (b) es el lado adyacente al ángulo del que queremos determinar.

Todos los triángulos considerados se encuentran en el Plano Euclidiano, por lo que la suma de sus ángulos internos es igual a π radianes (o 180°). En consecuencia, en cualquier triángulo rectángulo los ángulos no rectos se encuentran entre 0 y π/2 radianes. Las definiciones que se dan a continuación definen estrictamente las funciones trigonométricas para ángulos dentro de ese rango:
1) El seno de un ángulo es la relación entre la longitud del cateto opuesto y la longitud de la hipotenusa:

$\sin \alpha = \frac {{ \color{ForestGreen}\textrm{opuesto}}} {{ \color{Red}\textrm{hipotenusa}}} = \frac {a} {h}.$

El valor de esta relación no depende del tamaño del triángulo rectángulo que elijamos, siempre que tenga el mismo ángulo

α

, en cuyo caso se trata de triángulos semejantes.
2) El coseno de un ángulo es la relación entre la longitud del cateto adyacente y la longitud de la hipotenusa:

$\cos \alpha = \frac {{ \color{Blue}\textrm{adyacente}}} {{ \color{Red}\textrm{hipotenusa}}} = \frac {b} {h}.$

3) La tangente de un ángulo es la relación entre la longitud del cateto opuesto y la del adyacente:

$\tan \alpha = \frac {{ \color{ForestGreen}\textrm{opuesto}}} {{ \color{Blue}\textrm{adyacente}}} = \frac {a} {b}.$

4) La cotangente de un ángulo es la relación entre la longitud del cateto adyacente y la del opuesto:

$\cot \alpha = \frac {{ \color{Blue}\textrm{adyacente}}} {{ \color{ForestGreen}\textrm{opuesto}}} = \frac {b} {a}.$

5) La secante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto adyacente:

$\sec \alpha = \frac {{ \color{Red}\textrm{hipotenusa}}} {{ \color{Blue}\textrm{adyacente}}} = \frac {h} {b}.$

6) La cosecante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto opuesto:

$\csc \alpha = \frac {{ \color{Red}\textrm{hipotenusa}}} {{ \color{ForestGreen}\textrm{opuesto}}} = \frac {h} {a}.$

Sigue este ejemplo para entender un poco mas:

Teoremas del seno y del coseno

TEOREMA DEL SENO

TEOREMA DEL COSENO

domingo, 20 de febrero de 2011

RAZONES Y PROPORCIONES

¿Qué es la razón en geometría?
La razón como concepto geométrico viene definido así: Razón de dos números es el cociente indicado del primero entre el segundo

Es importante el orden en que se dicen o escriben los términos.
Se indica en forma de fracción.
Los dos números se llaman términos de la razón.
El primer termino se llama antecedente y el segundo termino consecuente.

¿Qué es la proporción?
La proporción es la igualdad de dos razones. Una proporción tiene por tanto cuatro términos ordenados:

Los cuatro números se llaman términos de la proporción
El primero y el ultimo se llama extremos y el segundo y el tercero se llaman medios.

¿Cuándo son dos razones iguales?

Dos razones son iguales cuando el producto de medios es igual producto de extremos.

Propiedades de las proporciones.

La suma de los antecedentes dividida entre la suma de consecuentes e igual a la razón de proporcionalidad.
En toda proporción la suma o resta de los dos primeros términos es al primero como la suma o resta de los dos últimos términos es al tercero.

lunes, 7 de febrero de 2011

THALES Y LA PROPORCIONALIDAD

SEMEJANZA DE TRIANGULOS

<><><><>




		En esta sección se analizará el concepto de semejanza de triángulos, con el fin de poder comprender su significado y aplicarlo en la solución de problemas. Antes de profundizar dicho concepto, se interiorizará solamente el concepto de semejanza. Para lo que se quiere realizar, es necesario el conocimiento de lo que son lados correspondientes y lo que es proporcionalidad, para ello considere la figura que se muestra abajo en la que los lados correspondientes son respecticamente: c y c' (lado grande y lado grande) a y a' (lado pequeño y lado pequeño) b y b' (lado mediano y lado mediano) Observe que al realizar la división entre los lados homólogos (correspondientes) el resultado que se obtiene es 2 (dividiendo 10 entre 5, 8 entre 4 y 6 entre 3), este valor recibe el nombre de razón y cuando la razón es igual en todos y cada uno de los lados correspondientes, se dice que los lados son proporcionales. El concepto de semejanza en la vida cotidiana Cuando se utiliza el término de semejanza en el lenguaje cotidiano, ¿a qué nos estamos refiriendo? Será acaso: Un objeto que se parece a otro Objetos de igual tamaño Objetos de igual forma Objetos exactamente iguales Es difícil poder seleccionar una opción que responda correctamente a la pregunta planteada, ya que de acuerdo al contexto de la conversación, el significado y utilización de la palabra semejanza, podría hacer referencia a objetos que se parecen en tamaño, forma o exactamente iguales, entre otros. Por ejemplo: El color del automóvil de Pedro es semejante al color del automóvil de María. La pelota de ping-pong es semejante a la de fútbol. La estatura de Marcela es semejante a la de Enrique. Los gemelos Baltodano Carrillo son tan semejantes que es difícil diferenciarlos. La llave que usa Sofía, para abrir la puerta de su casa, es semejante a la de su hermano José. Se podría seguir enunciando ejemplos, que ayuden a comprender el concepto de semejanza. Note que en los ejemplos mencionados, el significado de semejanza hace referencia a una característica común entre los objetos o personas, tales como: color, tamaño y forma, entre otros. Resumiendo: el uso del concepto de semejanza en el lenguaje cotidiano se refiera al "parecido", en una o más características, que existe entre dos personas u objetos. El concepto de semejanza en matemática El concepto de semejanza en matemática está muy ligado al concepto de proporcionalidad. En esta ciencia se dice que dos objetos son semejantes si "guardan" una proporción entre ellos. Veamos algunos ejemplos de la relación existente entre semejanza y proporcionalidad. Un geógrafo desea determinar la distancia entre dos ciudades, para ello utiliza un mapa. Se percata que la escala utilizada en el mapa es de 1:5000, es decir, un centímetro en el mapa representa 5000 metros en la realidad. Luego de medir con una regla la distancia entre las dos ciudades, obtiene que es de 3cm, lo cual representa 15000 metros en la realidad. Note que el mapa es una representación semejante a una porción del globo terráqueo, de allí que, deba guardar una misma proporción, con el fin de que las medidas que se tomen sobre él sean lo más cercanas a su valor real. La construcción de modelos a escala (aviones, barcos y edificios, entre otros) requiere de una buena aplicación de los conceptos de semejanza y proporcionalidad, esto con el fin de que la maqueta sea lo más semejante posible al objeto real, además de guardar una proporcionalidad adecuada, en otras palabras, el tamaño de cada una de sus partes debe estar acorde con el tamaño que el objeto tiene en la realidad. Dos fotografías de la misma persona, una de tamaño 3x4 pulgadas que luego es ampliada a 6x8 pulgadas. Ambas son semejantes y tienen una misma proporción, ya que una es la ampliación de la otra tanto a lo ancho como a lo largo y con una misma razón, o sea, las divisiones de sus lados correspondientes son de igual valor. Dos anillos idénticos, cuyos diámetros son exactamente iguales, guardan la misma proporción y semejanza entre cada una de sus partes (circunferencia, radio, área, diámetro). El último ejemplo refleja que siempre, dos objetos que son del mismo tamaño y forma se pueden catalogar como semejantes. Se debe tener cuidado con la afirmación inversa, es decir, objetos de diferente tamaño no son siempre semejantes, todo depende de que guarden o no la misma proporción, tal es el caso de los ejemplos uno, dos y tres. En otras palabras, para que dos objetos sean semejantes bajo la concepción matemática, no siempre tienen que ser iguales. Resumiendo: dos figuras son semejantes si guardan una proporción entre cada una de sus partes respectivas. Semejanza de triángulos Ya se ha estudiado el concepto de semejanza, tanto en lenguaje cotidiano como en leguaje matemático. Se aplicarán ambas definiciones para establecer el concepto de semejanza de triángulos. Se podría afirmar, con lo que ya se conoce, que dos triángulos son semejantes si poseen una misma forma y sus partes guardan una proporción. Veamos un ejemplo:

miércoles, 12 de enero de 2011

VECTORES Y SUS OPERACIONES

Definición de vector

Un vector fijo

es un segmento orientado que va del punto A (origen) al punto B (extremo)

Módulo del vector

Es la longitud del segmento AB, se representa por

Dirección del vector

Es la dirección de la recta que contiene al vector o de cualquier recta paralela a ella.

Sentido del vector

El que va del origen A al extremo B.

Dos puntos A y B determinan dos vectores fijos

, con sentido distinto, que se llaman vectores opuestos.

Un vector fijo es nulo cuando el origen y su extremo coinciden.

SUMA DE VECTORES

Para sumar dos vectores libres

se escogen como representantes dos vectores tales que el extremo final de uno coincida con el extremo origen del otro vector.

Regla del paralelogramo

Se toman como representantes dos vectores con el origen en común, se trazan rectas paralelas a los vectores obteniéndose un paralelogramo cuya diagonal coincide con la suma de los vectores.

Para sumar dos vectores se suman sus respectivas componentes.